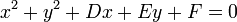Aprendiendo Matemáticas: 2012

sábado, 27 de octubre de 2012

martes, 16 de octubre de 2012

Circunferencia

Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan de otro punto fijo y coplanario llamado centro en una cantidad constante llamada radio

Ecuación en coordenadas cartesianas

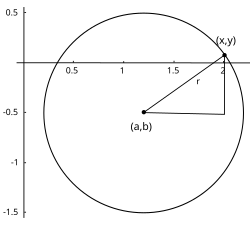
En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio r consta de todos los puntos (x, y) que satisfacen la ecuación

$(x-a)^2 + (y-b)^2 = r^2\,$ .

Cuando el centro está en el origen (0, 0), la ecuación anterior se simplifica al

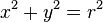$x^2 + y^2 = r^2\,$ .

La circunferencia con centro en el origen y de radio la unidad, es llamada circunferencia goniométrica, circunferencia unidad o circunferencia unitaria.
De la ecuación general de una circunferencia,

$(x-a)^2 + (y-b)^2=r^2 \,$

se deduce:

$x^2+y^2+Dx+Ey+F=0 \,$

resultando:

$a = -\frac{D}{2}$

$b = -\frac{E}{2}$

$r = \sqrt{a^2 + b^2-F}$

Si conocemos los puntos extremos de un diámetro: $(x_1,y_1), (x_2,y_2)\,$ ,
la ecuación de la circunferencia es:

$(x-x_1)(x-x_2)+(y-y_1)(y-y_2)=0.\,$

http://es.wikipedia.org/wiki/Circunferencia

martes, 9 de octubre de 2012

Regiones del plano determinadas por una circunferencia.

Al igual que la recta, la circunferencia divide al plano en tres regiones.

1. Puntos del plano que pertenecen a la circunferencia, o sea que verifican su ecuación.

2. Puntos del plano interiores a la circunferencia. Estos puntos cumplen que su distancia al centro de la circunferencia es menor que el radio.

3. Puntos del plano exteriores a la circunferencia. Estos puntos cumplen que su distancia al centro de la circunferencia es mayor que un radio.

Las tres regiones mencionadas forman una partición del plano, es decir que no tienen puntos en común y la unión de todas las regiones es igual al plano.

Fernández, W. “Matemática de bachillerato, 2º ano: núcleo común”

jueves, 4 de octubre de 2012

miércoles, 3 de octubre de 2012

¿Cuánto sabes de cuadriláteros?

martes, 2 de octubre de 2012

lunes, 1 de octubre de 2012

Teorema de Pitágoras

(Pitágoras de Samos (585a. C. – 495 a. C.) fue un filósofo y matemático griego)

Problema a resolver:

¿Cuánto alambre será necesario para cada tensor?

De la lectura y comprensión del problema podemos concluir que:

Se conoce la medida de los catetos de un triángulo rectángulo
Se pide calcular la hipotenusa de ese triángulo

No podemos traducir los datos del problema a ecuación, porque no conocemos por el momento ninguna relación entre las medidas de los lados de un triángulo rectángulo.

Relación de Pitágoras

Desde la antigüedad se conoce la relación que existe entre las

medidas de los lados de cualquier triángulo rectángulo y también son conocidas muchas formas de llegar a ella. Veamos una. Consideremos un triángulo rectángulo cualquiera, por ejemplo el ABC.

Podemos construir un cuadrado que tenga de lado justo lo que mide el cateto b, más lo que mide el cateto c, es decir b+c.

El área de este cuadrado será (b+c)²

Si ahora trazamos las hipotenusas de los triángulos rectángulos que salen tendremos:

el área del cuadrado es las misma que antes, se puede poner ahora como la suma de las areas de los cuatro triángulos rectángulos celestes (base por altura sobre dos) (b.c)/2 , más el área del cuadrado amarillo a².

Por lo que (b+c)² = a²+ 4(b.c)/2

Entonces (b+c)² = a² + 2bc

Desarrollando el primer miembro de la igualdad obtenemos:

b² + 2bc + c² = a² + 2bc

Simplificando: b² + c² = a²

Concluimos que: En todo triángulo rectángulo la medida de la hipotenusa al cuadrado es igual a la suma de los cuadrados de las medidas de los catetos.

Esta relación se conoce como relación de Pitágoras.

Podemos ahora traducir la información del problema del comienzo a ecuación ya que hemos encontrado una relación entre las medidas de los lados de un triángulo rectángulo

La resolvemos: a² = 3² + 4²